Notice 3Le jeu des sept allumettes |
- 1° Analyse du problème.
Pour que l’ordinateur J.R. 01 gagne, « doit arriver le premier à la somme 7 (en binaire 111) dans la deuxième phase. Pour s’assurer de cela, il doit d’abord arriver premier au total de 4, qui lui permettra de compléter toujours 7 quel que soit le jeu de l’adversaire (1 ou 2 allumettes remises). Pour s’assurer le total de 4, « doit être le premier à mettre 1, ce qui veut dire que l’ordinateur J .R. 01 doit être le premier à jouer dans la deuxième phase (qui consiste à remettre les allumettes sur la table, allumettes qui ont été enlevées durant la première phase).
Donc, dans la première phase, il faut que l’ordinateur J.R. 01 arrive à laisser sur la table la dernière allumette que l’adversaire est obligé de prendre. Pour s’assurer cette position, l’ordinateur J.R.01 devra d’abord arriver à enlever 3 allumettes de la première phase, choisissant de prendre, soit une, soit deux allumettes (donc l’ordinateur J.R. 01 gagnera toujours si l’adversaire est le premier à jouer).
Si, au contraire, c’est le J.R. 01 qui commence, la stratégie dans la préparation du programme sera celle d’essayer de le faire arriver, plus tôt ou plus tard, sur un des totaux stratégiques 3 ou 6 dans la première phase, 1 ou 4 dans la deuxième. Chaque fois que ceci se vérifie, le J. R. 01 gagne. - 2° Table de valeurs.
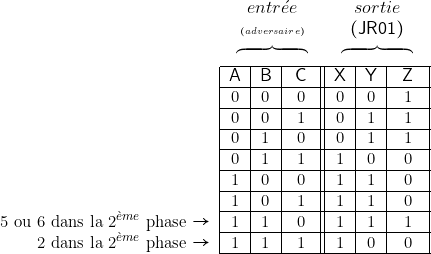
Les informations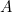 ,
, 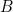 ,
, 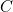 à l’entrée concernent le jeu de « l’adversaire », à la sortie
à l’entrée concernent le jeu de « l’adversaire », à la sortie  ,
, 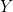 ,
, 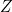 concernent le J.R.01.
concernent le J.R.01.- — Si
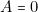 ,
, 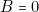 ,
, 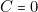 (c’est-à-dire si J.R. 01 commence, il enlèveune allumette (
(c’est-à-dire si J.R. 01 commence, il enlèveune allumette (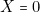 ,
, 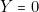 ,
, 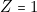 ) (1
) (1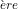 ligne dela table).
ligne dela table). - Si
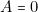 , B = 0,
, B = 0, 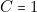 (une allumette enlevée par l’adversaire),J.R. 01 doit arriver au total de 3 donc
(une allumette enlevée par l’adversaire),J.R. 01 doit arriver au total de 3 donc 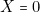 ,
, 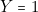 ,
, 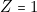 (car,en binaire, 011 équivaut à 3) (2
(car,en binaire, 011 équivaut à 3) (2 ligne de la table,page suivante).
ligne de la table,page suivante).
- — Si
- 3° Expressions algébriques.
La lampe est allumée (
est allumée (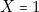 ) lorsque (Iignes 5 à 8)
) lorsque (Iignes 5 à 8)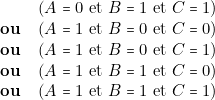 c’est-à-dire :
c’est-à-dire : 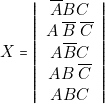
De même pour
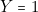 (lignes 2, 3, 5, 6,7), d’une part, et Z=1 (lignes 1, 2, 3, 7), d’autre part :
(lignes 2, 3, 5, 6,7), d’une part, et Z=1 (lignes 1, 2, 3, 7), d’autre part :
on a :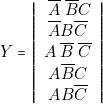
 et
et 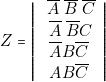
- Pour
 , écrivons :
, écrivons :
![Rendered by QuickLaTeX.com \[ X=\left|\begin{array}{c} \overline{A}BC\\ A\;\overline{B}\;\overline{C}\\ A\overline{B}C\\ AB\;\overline{C}\\ ABC \end{array}\right|=\left|\begin{array}{c} ABC\\ \overline{A}BC\\ AB\;\overline{C}\\ A\;\overline{B}\;\overline{C}\\ A\overline{B}C \end{array}\right|=\left|\begin{array}{c} BAC\\ B\overline{A}C\\ BA\;\overline{C}\\ A\;\overline{B}\;\overline{C}\\ A\overline{B}C \end{array}\right|=\left|\begin{array}{c} B\left|\begin{array}{c} AC\\ \overline{A}C\\ A\overline{C} \end{array}\right|\\ A\;\overline{B}\left|\begin{array}{c} C\\ \overline{C} \end{array}\right| \end{array}\right|=\left|\begin{array}{c} B\left|\begin{array}{c} A\\ C \end{array}\right|\\ A\;\overline{B} \end{array}\right|=\left|\begin{array}{c} BC\\ A \end{array}\right| \]](https://jr01.dhenin.fr/wp-content/ql-cache/quicklatex.com-28a9ff3fb52e7fe90979b08940af6b0b_l3.png)
- — Pour
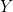 , écrivons :
, écrivons :
![Rendered by QuickLaTeX.com \[ {\scriptstyle Y=\left|\begin{array}{c} \;\overline{A}\;\overline{B}C\\ \overline{A}B\overline{C}\\ A\;\overline{B}\;\overline{C}\\ A\overline{B}C\\ AB\overline{C} \end{array}\right|=\left|\begin{array}{c} \overline{A}B\overline{C}\\ A\;\overline{B}\;\overline{C}\\ AB\overline{C}\\ \;\overline{A}\;\overline{B}C\\ A\overline{B}C \end{array}\right|=\left|\begin{array}{c} \left|\begin{array}{c} \overline{A}B\\ A\;\overline{B}\\ AB \end{array}\right|\overline{C}\\ \left|\begin{array}{c} \;\overline{A}\\ A \end{array}\right|\;\overline{B}C \end{array}\right|=\left|\begin{array}{c} \left|\begin{array}{c} B\\ A \end{array}\right|\overline{C}\\ \;\overline{B}C \end{array}\right|=\left|\begin{array}{c} \overline{C}B\\ \overline{C}A\\ \;\overline{B}C \end{array}\right|} \]](https://jr01.dhenin.fr/wp-content/ql-cache/quicklatex.com-4a374f02abfe94c0f2dc50503ef094b9_l3.png)
- — Pour
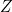 , écrivons :
, écrivons :
![Rendered by QuickLaTeX.com \[ Z=\left|\begin{array}{c} \;\overline{A}\;\overline{B}\;\overline{C}\\ \;\overline{A}\;\overline{B}C\\ \overline{A}B\overline{C}\\ AB\overline{C} \end{array}\right|=\left|\begin{array}{c} \;\overline{A}\;\overline{B}\left|\begin{array}{c} \overline{C}\\ C \end{array}\right|\\ \left|\begin{array}{c} \overline{A}\\ A \end{array}\right|B\overline{C} \end{array}\right|=\left|\begin{array}{c} \;\overline{A}\;\overline{B}\\ B\overline{C} \end{array}\right| \]](https://jr01.dhenin.fr/wp-content/ql-cache/quicklatex.com-3f9620992a2eb87bd244d4f55fa46b91_l3.png)
- 5° Schéma du programme (voir notice
 )}
)}
- Puisque
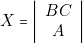 on doit relier la lampe
on doit relier la lampe  à deux « colonnes » de programmation.
On a choisi les colonnes 1 et 2.
à deux « colonnes » de programmation.
On a choisi les colonnes 1 et 2.
Sur la colonne 1, la fiche placée à gauche, sur la barrette
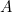 ,représente
,représente 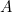 ; les fiches placées sur les barrettes
; les fiches placées sur les barrettes 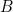 et
et 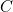 de part et d’autre de la colonne 1, « neutralisent »
de part et d’autre de la colonne 1, « neutralisent » 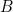 et
et 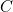 .
Donc, la colonne 1 « représente » A.
.
Donc, la colonne 1 « représente » A. La colonne 2 représente B . C (A est « neutralisée »). D’où
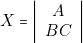
- — Pour obtenir
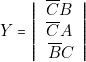 il faut relier la lampe
il faut relier la lampe 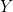 à trois « colonnes » de programmation.
à trois « colonnes » de programmation.
Nous avons choisi les colonnes 3, 4, 5.
Sur la colonne 3,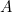 est « neutralisé » par les deux fiches, et les deux autres fiches « en série » représentent
est « neutralisé » par les deux fiches, et les deux autres fiches « en série » représentent 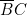 .
.
Sur la colonne 4, on a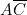 . Sur la colonne 5, on a
. Sur la colonne 5, on a 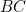 .
. - — Pour obtenir
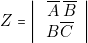 il faut relier
il faut relier 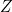 à deux « colonnes » de programmation.
à deux « colonnes » de programmation.
Sur la « colonne » 6, on a « neutralisé »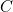 par deux fiches et on a « écrit »
par deux fiches et on a « écrit » 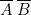 avec les deux fiches placées, à droite de la colonne, sur les barrettes
avec les deux fiches placées, à droite de la colonne, sur les barrettes 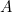 et
et 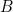 .
.
Sur la colonne 7, on a de même,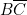 .
. - — Ainsi se trouve justifié le programme de la notice

- Puisque

